The Infinity of ONE

The Infinity of ONE is revealed by the nature of reiterated root calculations.

Overview

The number ONE has unique qualities, whereby an infinite boundary is formed around it when root calculations are reiterated. This gives it qualities similar to the number zero that forms a boundary through division of a number. Together the numbers +ONE, -ONE, and ZERO divided the number line into four distinct sections. Positive and negative whole numbers, and their respective reciprocal values. This principle applies to all powers and roots beyond x² and ²√x. When we examine the nature of powers and root equations, we find they are best represented geometrically. In this way, we see that a power is actually a 'shift in dimension' in terms of numbers, and so cannot be represented on the single dimension of a number line. This has deep reaching implications for the number i, that is founded upon the notion of √-1, but does not presently accommodate higher dimensional numbers, such as ³√-1.

KEy Points

• When we find the root of any number between ONE and infinity, the reuslt will always be greater than ONE.
• When we find the root of any number between ZERO and ONE the result will move closer to ONE by will never be greater than ONE.
• All root calculations will ‘move the result close to ONE but will never be able to cross the boundary of ONE.

THE

Concept

Root Boundaries

The number one is a special kind of number that divides reciprocal space and whole number space. Similar to the boundary of ZERO, the number ONE produces the unique quality in that no root calculation can cross its boundary.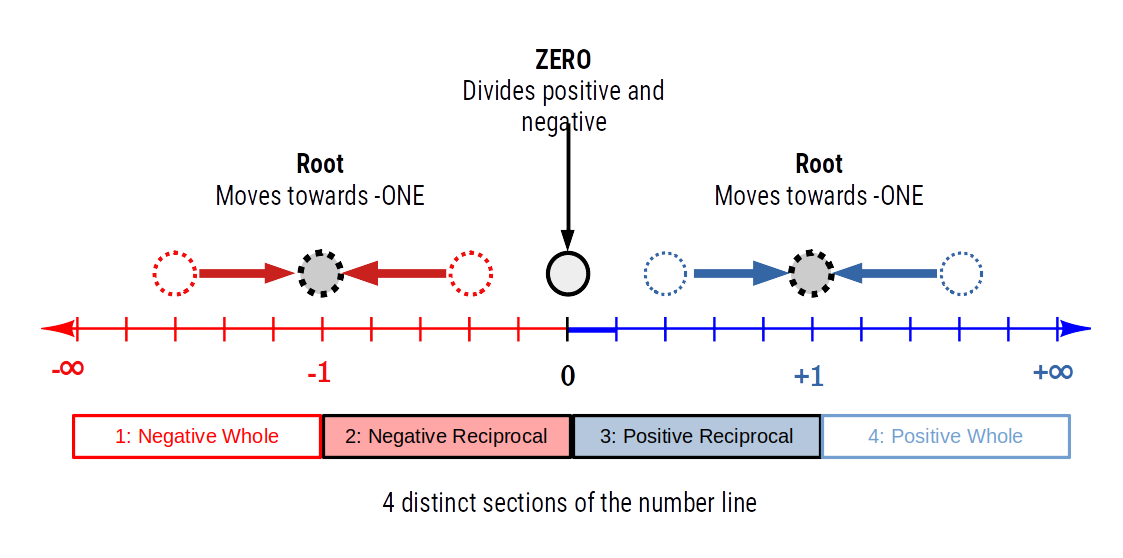

NOTICE: reciprocal root calculations produce a result that is closer to ONE, whereas division of a reciprocal results in a value closer to ZERO. Therefore, divisions and roots are NOT that same thing.

This means that the number one and number zero are spacial quantities that act to separate the number line into distinct, 4 distinct parts. Positive and negative whole numbers, and their respected reciprocal counter-parts.

Key point

The Infinity of ONE divides the number line into 4 parts This points to an interesting observation. The numbers ONE and ZERO, are only numbers to create these kinds of boundary when performing simple calculations. This means that all other numbers, including fractions, are of a different nature. The fact that reciprocal space between ONE and ZERO contains all numbers except ONE and ZERO is further confirmation of this difference. This raises the question as to the origin of all other numbers other than ONE and ZERO.

The Roots of Infinity

A root calculation involves one or more quantities of the same value. Just as a quantity can be squared, so we can find its square root. However, root calculations are not just applicable to squares. We can 'cube' a number by multiplying three equal numbers together. Similarly, we can find a cube root. In fact any number of equal numbers can be multiplied together, and by counting the number of multipliers we get the 'power' of the equation, described mathematically as x^x. The same goes for root values that are express as ^x√x. So there are also cube roots. In fact, we can take a number up to the power of infinity (x^∞) and even do the same for its root (^∞√x.)

There are an infinite number of roots and powers for each and every whoLe and fractional number

Finding the Infinity of ONE

Whole Number

We can easily find the infinity of ONE using a simple calculator. Make sure it has a square root button. To begin, enter a number greater than ONE. Press the square root button. Notice the answer will have moved closer to ONE, but will not be less than one. Press the square root button again. Again the number will diminish towards ONE but will never get less than ONE.

Reciprocal Number

We can do the same for any value between ZERO and ONE. Just choose an appropriate number and keep rooting the value. Notice that the value increases towards ONE. Yet, no matter how many times we repeat the process, we will never be able to produce a result greater than one.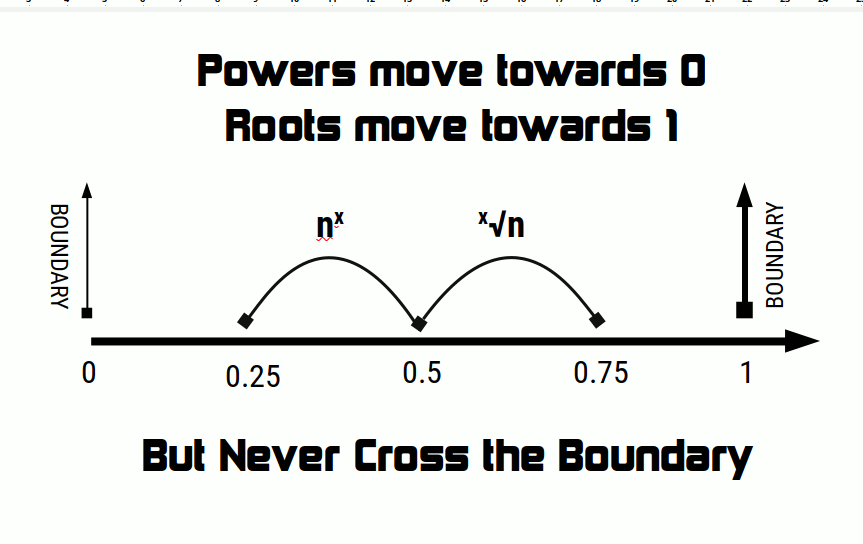

*NOTE: if your calculator does go to ONE, then it is because it has run out of memory, and so can't calculate the correct value. Computers don't do infinity.

Geometric powers and roots

The defining fact about a number that is raised to a particular power is that the quantities are equal. This is best explored as a geometric concept.

Rotation around ZERO

If we think the notion of 'squaring' geometrically, it makes perfect sense. When a value is squared, then the number line becomes rotated at 90°. This normally occurs around the zero point, to form the geometry of a square*. A similar principle applies to a cubed number that adds a third number line (z-axis) rotated in 3D space. When we take a number to higher power, we are adding greater dimensionality to the result.  Due to this, numbers that are raised to any power cannot actually be described on a one dimensional number line. So where are they described?

The number line squared? But what about the negative numbers?

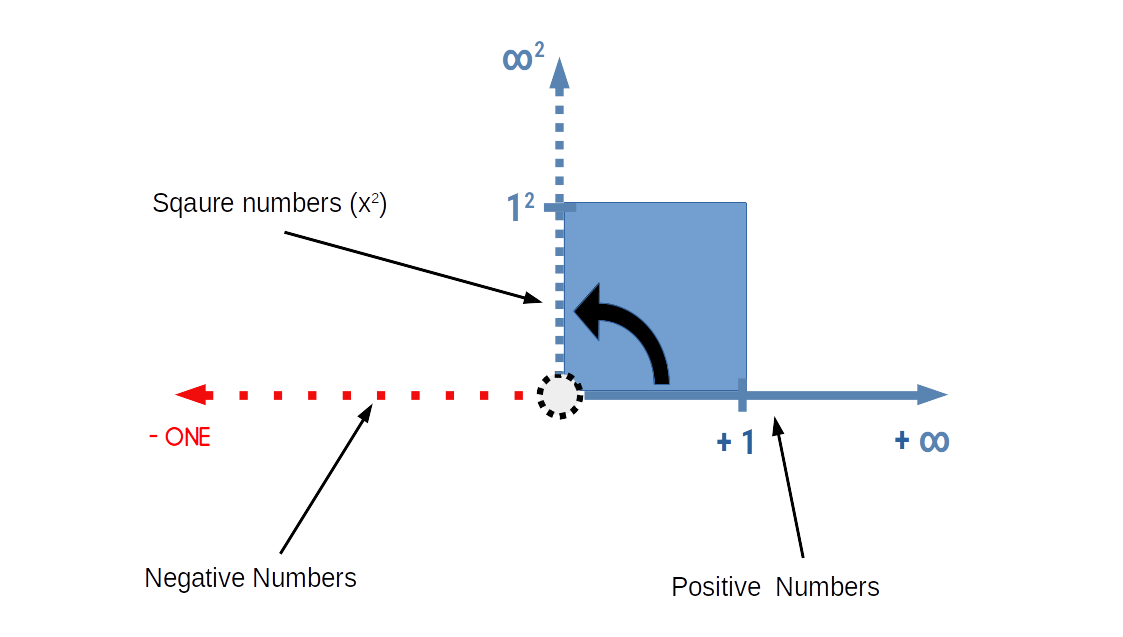
*Notice that in this traditional view of square numbers, the negative line does not rotate. This is one of the fundamental differences of the new mathematics proposed by in2infinity.

FIND OUT MORE ABOUT NEGATIVE SQUARE NUMBERS LEARN MORE

Key point

Powers and roots are geometric in nature and cannot be expressed on a number line

Implications for the number 'i'

The number i is a mathematical concept that is the expression of √-1. This in turn gives rise to the 'complex number plain' which is supposed to encapsulate all possible number types. However, mathematical proof to support this claim has yet to be formulated.

More than i can see

Powers and roots can be seen to be opposite functions of each other. When we square a number, so the result can be rooted, and the original number obtained. The number i only expresses one out of an infinite number of roots and powers, both in the positive and the negative. Therefore, it cannot be considered to offer a complete picture of number theory. This has wide-ranging implications for the foundations of modern mathematics, especially in relation to the present day solution to the Continuum Hypothesis, which we suggest is incomplete.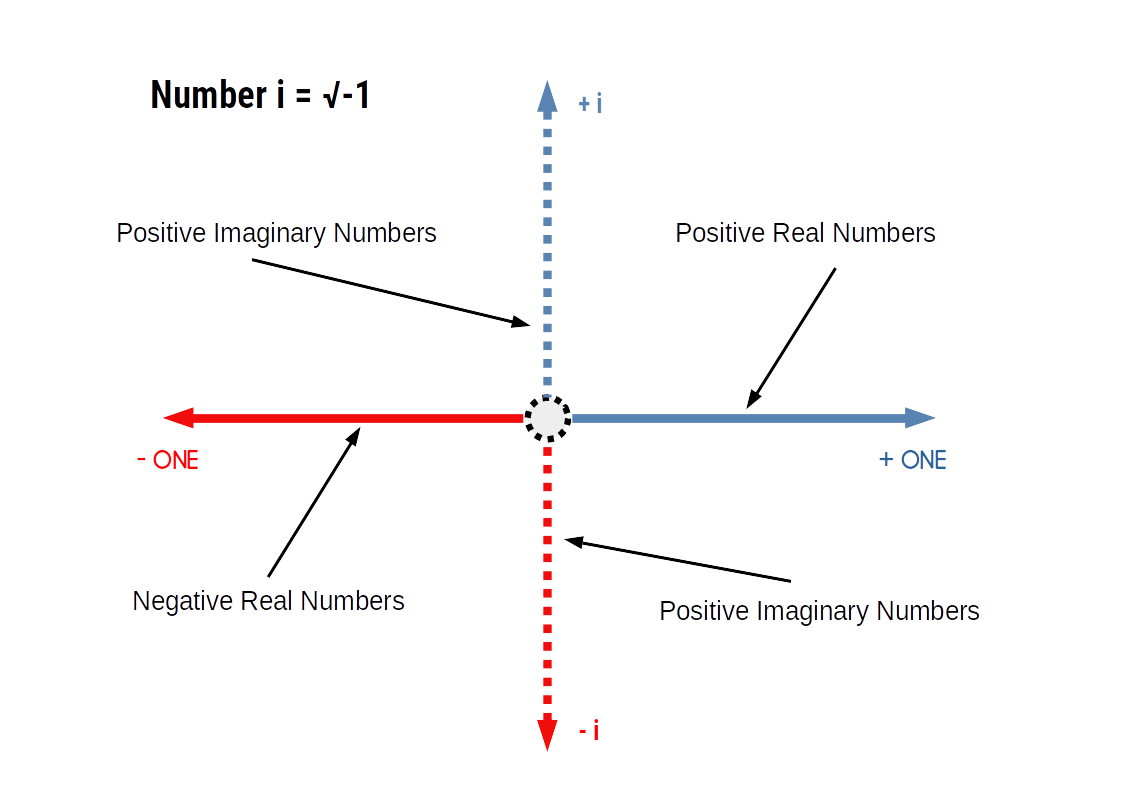

The number 'i' was invented to compensate for the fact the square root of minus one did not appear on the number line. Whilst current beliefs suggest that the number i completes our mathematical theory of numbers, we point out that we have yet to define the greater powers such as ³√-1, and more

THE

Conclusion

So what does this tell us about ONE?

The number one is no ordinary number. It forms a boundary similar to the number zero. The difference is that whilst the boundary of zero is revealed when a number is divided, The boundary around ONE only becomes apparent through calculations involving powers and roots.

Where did all the powers go?

Powers and roots are geometric in nature. The number i also employs a rotation of the number line to form its axis. However, as its foundation is the √-1 it cannot accommodate numbers of a higher power.

Carry On Learning

This article is part of our new theory, 'Maths of Infinity'

Read the main article or browse more interesting post from the list below

YOUR QUESTIONS ANSWERED

Got a Question? Then leave a comment below.

SARAH

Question?

Hold on, What about negative numbers, they don't form a negative squares?

ANSWER?

Actually, in our new geometrical theory of mathematics, we do. Traditional mathematics cannot define a negative square number due to the way it has been defined. See our post on 'negative square numbers' for more details.

HILERY

Question?

Is a cube root the diagonal of a cube?

ANSWER?

Actually, it tells us the side length of a cube that has a specific volume. The diagonal of a square is found through the square root of 2, and the diagonal of a cube is found through the square root of 3. You can multiply the side length by either of these two factors to find the respective diagonal.

Sharing is Caring

View Original Article